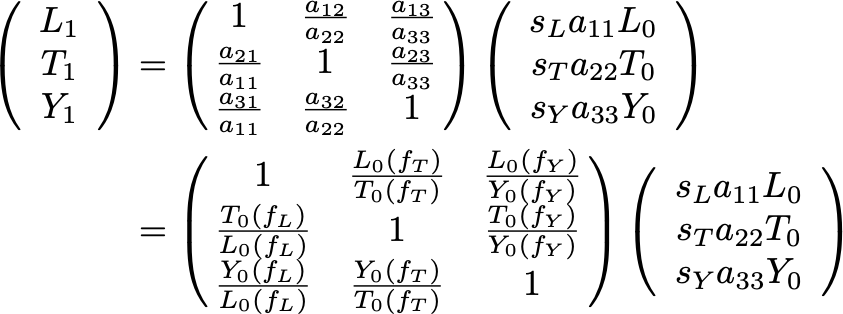|
Size: 1547
Comment:
|
Size: 1579
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 15: | Line 15: |
| [[attachment:eq_matrix.png]] | {{attachment:eq_matrix.png}} |
| Line 19: | Line 19: |
{{attachment:diagimage.png}} |
2019/03/28
What we did
- センサーの対角化を進める。
数学的背景
- 進める前に,センサーの対角化について数学的にどうなるかをまとめておこう。
- ゴールは,「各自由度が分離できる」「自由度ごとにどれだけ振れるかの大きさを把握する」こと
- 後述するが,2つ目の目標は,絶対的な大きさまで把握しようとすると難しい。
- TMS-VISは剛体の6自由度だが,まず簡単のために水平方向の3自由度(Longitudinal, Transverse, Yaw)で考える。
- センサーの幾何学的配置からある程度自由度が分離できているとして,その自由度の基底を(e_Lg, e_Tg, e_Yg)^tとする。このセンサーで得た各自由度のスペクトルを(L_1, T_1, Y_1)
- 目標の理想的な,真の自由度の基底を(e_Li, e_Ti, e_Yi)^tとする。真の自由度で測定できた場合の各自由度のスペクトルを(L_0, T_0, Y_0)
- 対角化のイメージとしては,これら(L_1, T_1, Y_1)と(L_0, T_0, Y_0)との変換行列を求めることである。
- ここで,幾何学的配置からのセンサーは真の自由度に近いとするという近似をする。つまり,上の行列の対角成分は1であるとする。
- また,真の自由度からのスペクトルは測定できないが,それに対して何かしら定数倍がかかっているものは測定できるとする。