|
Size: 3474
Comment:
|
Size: 3478
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 41: | Line 41: |
| f1 = q*c/(4*Lprc)<<BR>> f2 = p*c/(4*Lprc) |
f1 = p*c/(4*Lprc)<<BR>> f2 = q*c/(4*Lprc) |
| Line 50: | Line 50: |
| If Lprc is changed to Lprc2 = Lprc + dL, then a new f1 frequency f1d has to be chosen to still resonate it in the PRC. Since, f1d = q*c/(4*Lprc2), 1/f1d = 1/f1 + 4*dL/(q*c). Therefore, the new SRC length (Lsrc2) to resonate f1 in the SRC is: | If Lprc is changed to Lprc2 = Lprc + dL, then a new f1 frequency f1d has to be chosen to still resonate it in the PRC. Since, f1d = p*c/(4*Lprc2), 1/f1d = 1/f1 + 4*dL/(p*c). Therefore, the new SRC length (Lsrc2) to resonate f1 in the SRC is: |
| Line 52: | Line 52: |
| Lsrc2 = n*c/(2*f1d) - Lprc2 = Lsrc + 2*n*dL/p. | Lsrc2 = n*c/(2*f1d) - Lprc2 = Lsrc + 2*n*dL/p -dL. |
Layout related issues
Contents
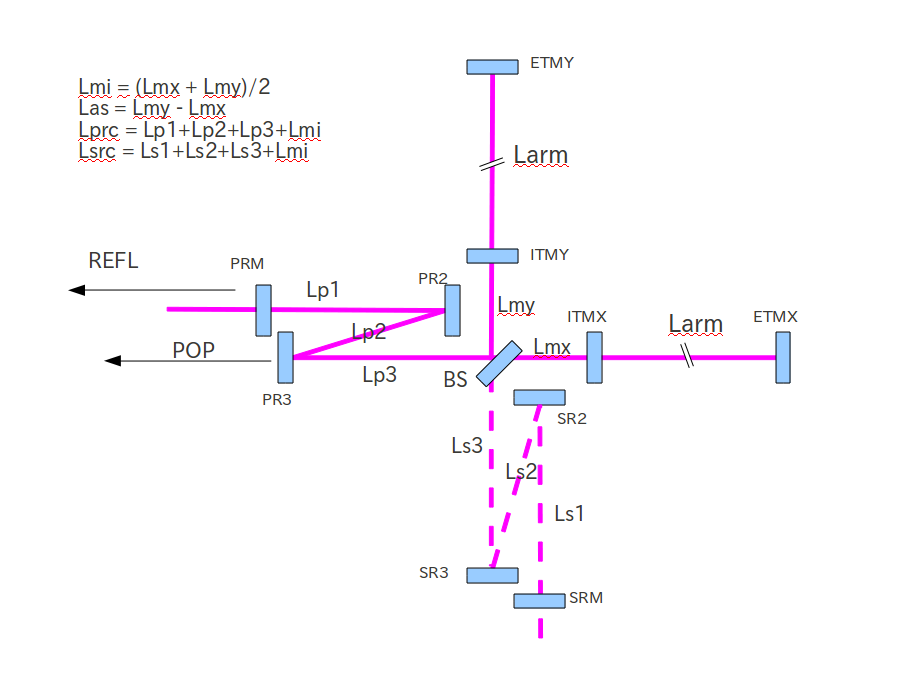
Location of PR2 tank
Is it possible to put the PR2 and SR2 vacuum chambers further away from the BS chamber ? The minimum separation is 2.7m (center-to-center). However, in order to improve the workability around the BS chamber, we want increase the separation.
Comparison Table
L_BS_PR2 is the separation between the center of BS chamber and the center of PR2 chamber. The following table shows the the Folding parameters with three different cases of L_BS_PR2. Case 1 is the default plan. Case 2 adds 2m to the BS-PR2 separation, and Case 3 adds 3m.
Note that the arm cavity g-factor is assumed to be negative (1.5km-1.9km), which usually gives slightly smaller beam sizes on the PRM.
|
L_BS_PR2 |
Folding Angle |
Lp1 |
Lp2 |
Lp3 |
PRM ROC |
PRM Beam Size |
PR2 ROC |
PR2 Beam Size |
PR3 ROC |
PR3 Beam Size |
Case 1 |
2.7m |
0.63deg |
14.76m |
12.07m |
14.76m |
310.42m |
4.05mm |
-3.13m |
4.05mm |
27.01m |
35.43mm |
Case 2 |
4.7m |
0.67deg |
14.09m |
11.40m |
16.10m |
295.3m |
3.95mm |
-2.88m |
3.95mm |
25.45m |
35.46mm |
Case 3 |
5.7m |
0.69deg |
13.76m |
11.06m |
16.76m |
287.75m |
3.91mm |
-2.75m |
3.91mm |
24.67m |
35.48mm |
Layout files
The optical layout files corresponding to the above cases.
iLCGT -> bLCGT PRCL/SRCL change due to the substrate change
Because the substrate material will be changed from Silica to Sapphire between iLCGT and bLCGT, the index of refraction change will induce the optical path length change of PRC and SRC. We can cancel this change by simply moving the ITMs. Probably we will do this. However, a question to be answered here is whether it is possible to cancel the change by changing the MC length and consequently changing the f1/f2 frequencies.
In short, the answer to the question is "Yes".
In general, it is not possible to satisfy the resonant condition of PRC and SRC at the same time, just by changing the MC length. Once the Lprc is given, the RF sideband frequencies are given as follows,
f1 = p*c/(4*Lprc)
f2 = q*c/(4*Lprc)
,where p, q are integral numbers and c is the speed of light.
Now, once the f1 frequency is given, the length of SRC is given in the following form:
Lsrc = n*c/(2*f1) -Lprc
,where n is an integer. The MC length is given as Lmc = 2*Lprc/a, a = GCD(p,q).
If Lprc is changed to Lprc2 = Lprc + dL, then a new f1 frequency f1d has to be chosen to still resonate it in the PRC. Since, f1d = p*c/(4*Lprc2), 1/f1d = 1/f1 + 4*dL/(p*c). Therefore, the new SRC length (Lsrc2) to resonate f1 in the SRC is:
Lsrc2 = n*c/(2*f1d) - Lprc2 = Lsrc + 2*n*dL/p -dL.
This means, if n = p, Lprc2 = Lsrc + dL, meaning that f1d automatically resonates in the SRC. This is not the case in general. However, if we chose n to make Lprc = Lsrc, then n = p is automatically satisfied. The current length parameters of LCGT falls into this category. Therefore, it is possible to cancel the optical distance change by the substrate change of ITMs just by changing the MC length.
