• KAGRA
• Subgroups
• CAL
• GstLAL
• tutorials
• step6a

Step 6a: Make FIR

This tutorial describes how a time-domain filter can be created based on theoretical Z, P and K values. In particular, a process of generating a combined response of the inverse analog and digital anti-aliasing (AA and dAA) filters is shown. <ul>

• The python script that implements the process described on this page is based on "Step 6".</li> <li>Responses of the AA^-1 and dAA^-1 are expressed with zeros and poles as follows:

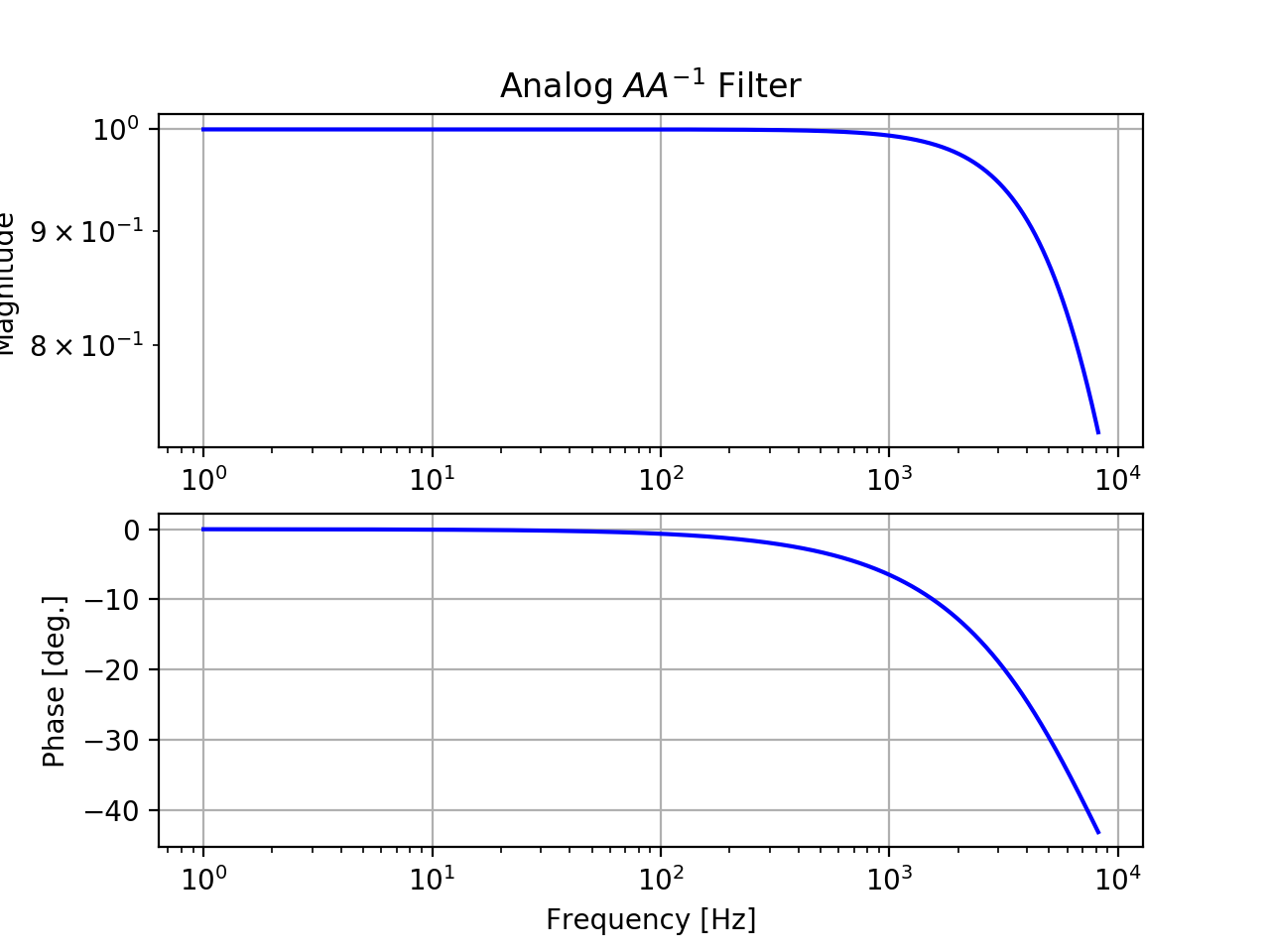
  • * Inverse of the analog AA filter:
    • Zeros: [7680.37]
    • Poles: [8190, 8190]
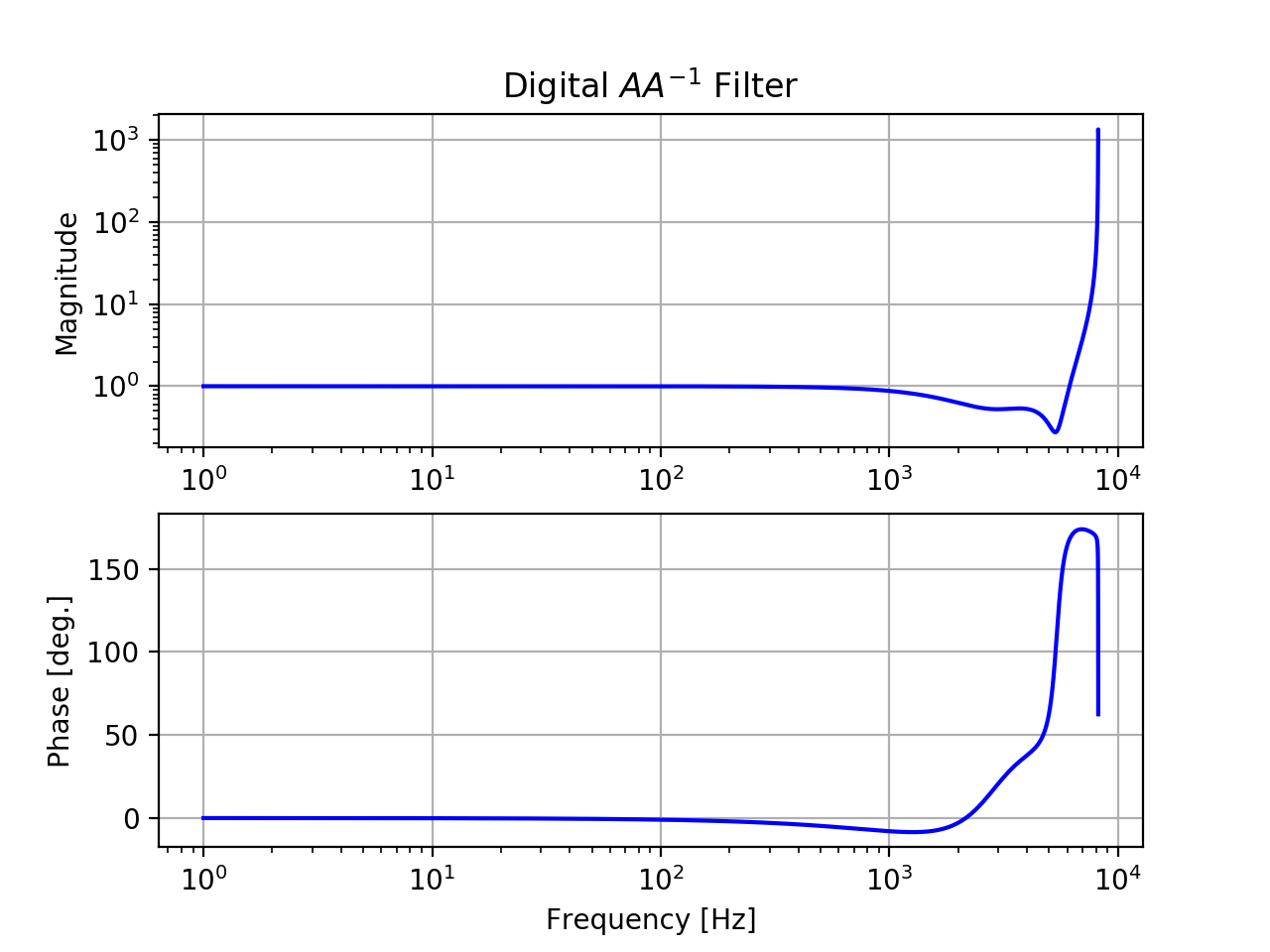
  • * Inverse of the digital AA filter:
    • Zeros: [1272.9+1j*2600.52, 1272.9-1j*2600.52, 352.852+1j*5384.07, 352.852-1j*5384.07]
    • Poles: [6.14865+1j*8190, 6.14865-1j*8190, 6000, 6000, 6000]
• In a python script these parameters are described as follows (the example shows the analog AA parameters):

# inverse of the analog Anti-Aliasing (AA^-1)
dsgn_AA_z = [7680.37]
dsgn_AA_p = [8190, 8190]

• The scipy.singal package can be used to create an LTI object with these parameters. Below is a python function that creates an LTI object from zeros and poles expressed in Hz and a gain:

def myZPKhz(z, p, k):
    z2pi = [-2 * np.pi * x for x in z]
    p2pi = [-2 * np.pi * x for x in p]
    g = k * np.prod(p2pi) / np.prod(z2pi)
    return sg.lti(z2pi, p2pi, g)

• E.g. an LTI system of the AA^-1 is creates as shown below:

dsgn_AA = myZPKhz(dsgn_AA_z, dsgn_AA_p, 1.0)

• One can obtain frequency response from an LTI object and generate FIR filter coefficients of a corresponding time-domain filter. These steps are described in a previous tutorial.
• Scripts for this tutorial were committed to kagra-cal repository at "gstlal-kagracal/tests/TDFilters/*"

Output

• The script "td_genFIR_AA_dAA" calculates FIR filter coefficients and saves them in an ".npz" file.

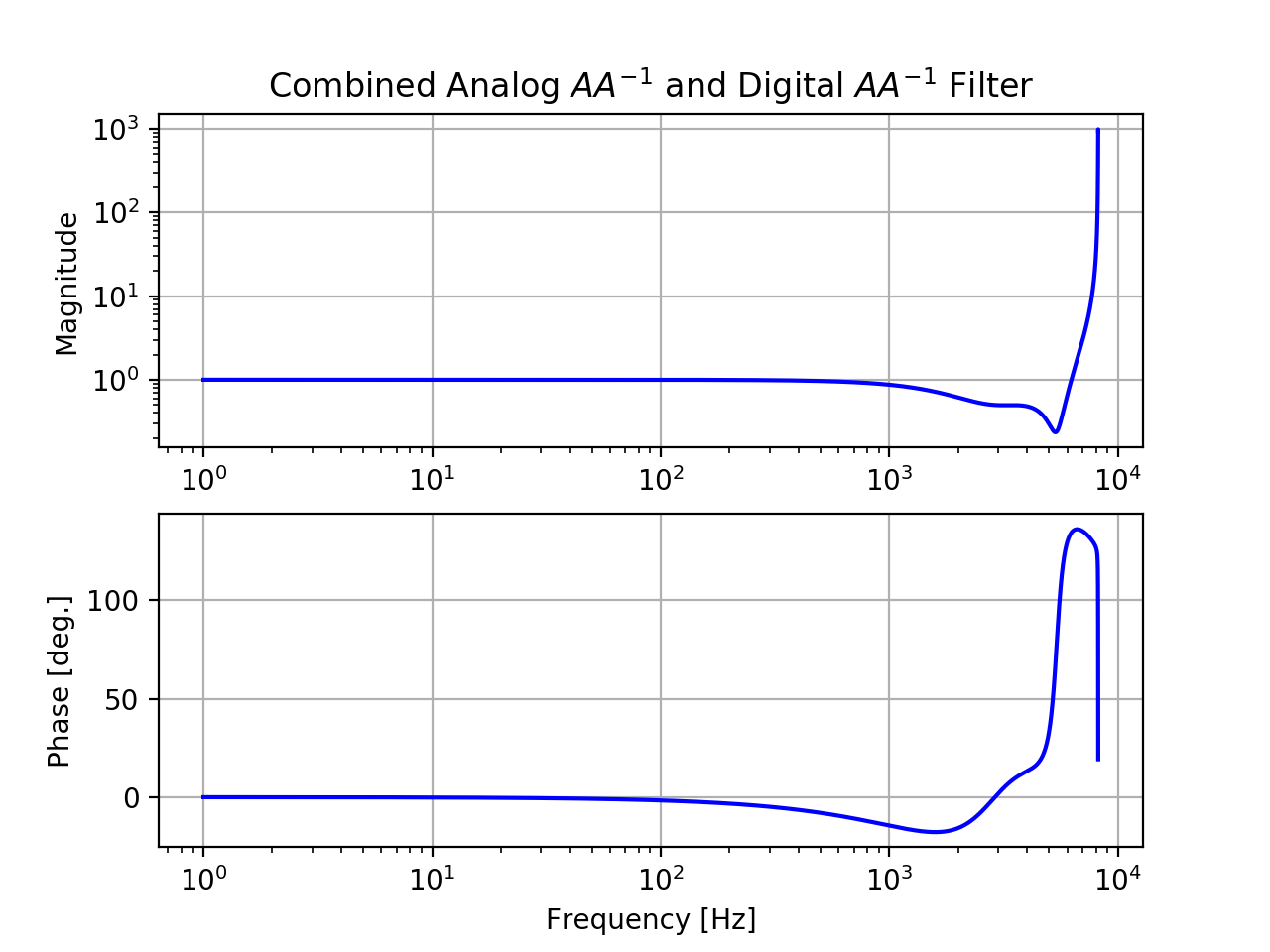
• Frequency responses of AA^-1 and dAA^-1 and the two combined are shown below:

  •