Step 6: Make FIR filters and save into a npz file
- We assume a simple DARM model with
- Actuation (A) with f^{-2} (fc=0.7, Q=100) and delay of 61 us x2
- Sensing (C) with frequency independent and delay of 61 us
By importing scipy.signal we can construct and manipulate LTI models easily.
- Here is a small piece of python code to represent a f^{-2} pole
1 # Convert f0 and Q to a pair of complex numbers
2 def fq2c(f0, Q, rad=False):
3 w0 = -f0 if rad else -2*np.pi*f0
4 a = w0/(2*Q)
5 b = w0/(2*Q)*np.sqrt(4*Q**2-1)
6 return np.array([a+1j*b, a-1j*b])
7
8 # Complex-conjugate pair of poles at f with Q and the DC gain = gn
9 def pole2(f, Q, gn=1, dt=0, rad=False):
10 (a,b) = fq2c(f, Q, rad);
11 w1 = 2j*np.pi
12 g0 = abs(1/(w1-a)/(w1-b))
13 return sg.lti([], [a,b], gn/g0, dt=dt)
- Here is the part to define DARM model parameters
1 fNyq = 8192 # Nyquist frequency
2
3 # Actuation model
4 f0 = 0.7 # pole frequency
5 Q = 100 # pole Q
6 gn = 0.917e-10 # actuation gain (m/ct)
7 tda = 2*(1./2)**14 # actuation delay (2 digits)
8 Tla = 2. # Length of time-domain filter in second
9 fca = 4. # High-pass filter frequency
10 dla = Tla*fNyq
11 act = pole2(f0, Q, gn)
12
13 # Inverse sensing model
14 C = 9.356e-12 # inverse optical gain (m/ct)
15 tdc = (1./2)**14 # sensing delay (1 digit)
16 Tlc = 0.5 # Length of time-domain filter in second
17 fcc = 8. # High-pass filter frequency
18 dlc = Tlc*fNyq
19 sen = sg.lti([], [], C)
- Here is the part to generate the FIR filter and save to npz (numpy zipped) file
- Another python script gentd.py contains the actual part to generate time-domain FIR filter
- Here is a core part of gentd.py. It is just an inverse-FFT from frequency response data into time domain
- Please note that high-pass filter is applied at the frequency specified by fcut. This is needed to minimize the FIR filter length to get reasonable computation time
1 # Generate time domain FIR filter of LTI system
2 def gentd(sys, td=0, fcut=4, Tl=2, fNyq=8192):
3 ...
4 # Apply Hann window to roll off low frequencies
5 h[0:2*hp] = h[0:2*hp]*cond[0:2*hp]
6
7 h[0] = 0 # Zero out the DC component
8 h[Nf-1] = 0 # Zero out the Nyquist component
9
10 # Apply delay
11 delay = np.exp(-1j*w*(np.floor(Tl*fNyq)*dt+td))
12 h = h*delay
13
14 # Fill out negative frequencies
15 for k in np.arange(0, Nf-2):
16 h = np.append(h, np.conj(h[Nf-k-2]))
17
18 # Take inverse Fourier transform
19 td = np.fft.ifft(h)
20 td = td.real-td[0].real
- The python script is available at git repository
> kagra-cal/Observation/Phase1/tutorials/genfl
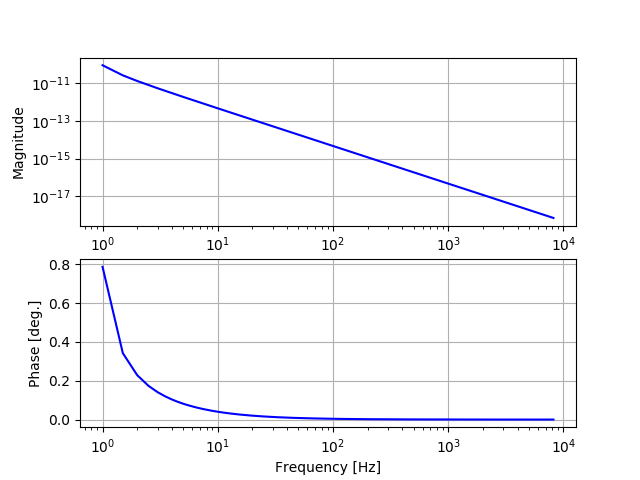
- The bode plot shows the the frequency response of the actuation filter
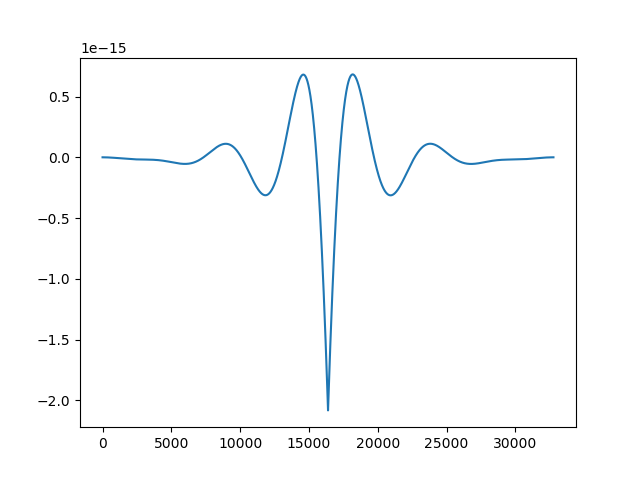
- Check the contents of the output file (filt.npz)
> python
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> fig=plt.figure()
>>> fl=np.load('filt.npz')
>>> plt.plot(fl['a'])
>>> fig.show()
>>> plt.savefig('afilt.png')- The plot shows the time domain FIR coefficients (= impulse response) for the actuation filter